Parte Teorica S.POTENCIA 2012 09 S1 (Cadena abierta, cadena cerrada; Variables de salida)

Resolucion:

Control en cadena abierta y en cadena cerrada viene en el apartado 18.4 del Libro.

Modos de cambio de variable de salida: Control todo o nada, cambio de estados discretos y regulacion continua vienen en el apartado 18.5 del libro.

‹ Cuestion 2 S.POTENCIA 2012 09 S1 (Convertidor de cuatro cuadrantes)arriba2012 09 S2 EXAMEN S.E.POTE

Calcular densidad fluido (gas) con el programa matematico SAGE

Funcion para calcular la densidad de un fluido (gas) a partir de la temperatura en grados centigrados y la presion en pascales con el programa / software matematico Sage. Como ejemplos el hidrogeno, el oxigeno y el vapor de agua

El programa en el software matematico Sage para obtener la densidad:

def densidadfluido(P,Matom,T):

r=P*Matom/(101325*0.082*(273+T))

return(r)

Matom_O2=16*2 # Masa atomica del oxigeno O2

T_O2=27       # Temperatura en grados centigrados del oxigeno O2

P_O2=1.5*10^5 # Presion en pascales del oxigeno O2

Matom_H2=1*2 # Masa atomica del hidrogeno H2

T_H2=27       # Temperatura en grados centigrados del hidrogeno H2

P_H2=1.5*10^5 # Presion en pascales del hidrogeno H2

Matom_H2O=1*2+16 # Masa atomica del vapor de agua H2

T_H2O=200       # Temperatura en grados centigrados del vapor de agua H2O

P_H2O=10^5 # Presion en pascales del vapor de agua H2O

densidadfluido(P_O2,Matom_O2,T_O2),densidadfluido(P_H2,Matom_H2,T_H2),densidadfluido(P_H2O,Matom_H2O,T_H2O)

Resultado:

(1.92570393505563, 0.120356495940977, 0.458016263623169)

‹ Ejemplos con SAGEarribaCalcular densidad fluido (gas) con el programa matematico SAGE ›

Calcular densidad fluido (gas) con el programa matematico SAGE

Funcion para calcular la densidad de un fluido (gas) a partir de la temperatura en grados centigrados y la presion en pascales con el programa / software matematico Sage. Como ejemplos el hidrogeno, el oxigeno y el vapor de agua

El programa en el software matematico Sage para obtener la densidad:

def densidadfluido(P,Matom,T):

r=P*Matom/(101325*0.082*(273+T))

return(r)

Matom_O2=16*2 # Masa atomica del oxigeno O2

T_O2=27       # Temperatura en grados centigrados del oxigeno O2

P_O2=1.5*10^5 # Presion en pascales del oxigeno O2

Matom_H2=1*2 # Masa atomica del hidrogeno H2

T_H2=27       # Temperatura en grados centigrados del hidrogeno H2

P_H2=1.5*10^5 # Presion en pascales del hidrogeno H2

Matom_H2O=1*2+16 # Masa atomica del vapor de agua H2

T_H2O=200       # Temperatura en grados centigrados del vapor de agua H2O

P_H2O=10^5 # Presion en pascales del vapor de agua H2O

densidadfluido(P_O2,Matom_O2,T_O2),densidadfluido(P_H2,Matom_H2,T_H2),densidadfluido(P_H2O,Matom_H2O,T_H2O)

Resultado:

(1.92570393505563, 0.120356495940977, 0.458016263623169)

‹ Calcular densidad fluido (gas) con el programa matematico SAGEarribaCalcular el conjugado de un numero complejo con SAGE ›

Control predictivo

   


‹ CONTROL ADAPTATIVOarribaCatalogos de Regulacion Automatica ›

SOLDADURA

Comienzos con soldadura en arco



















arribaComienzos con soldadura en arco ›

Comienzos con soldadura en arco

• 1 Soldadura horizontal con arco
• 2 Soldadura en angulo con arco
• 3 Soldadura con arco en horizontal en pared

‹ SOLDADURAarriba1 Soldadura horizontal con arco ›

1 Soldadura horizontal con arco

Video de soldadura con arco piezas en horizontal mediante media luna, picado del electrodo, angulos de soldado.












‹ Comienzos con soldadura en arcoarriba2 Soldadura en angulo con arco 

2 Soldadura en angulo con arco

Video de soldadura con arco de dos piezas en angulo mediante L, angulos de soldado.























‹ 1 Soldadura horizontal con arcoarriba3 Soldadura con arco en horizontal en pared ›

3 Soldadura con arco en horizontal en pared

Video de soldadura en horizonta en pared de dos piezas en con dibujo en muelle o e, angulos de soldado.

Concatenar / unir vectores con Scilab

Vamos a unir o concatenar dos vectores con Scilab

-->u1=zeros(1,3);

-->u2=ones(1,4);

-->u=[u1,u2];

-->u

 u  =

         column 1 to 6

    0.    0.    0.    1.    1.    1.  

         column 7

    1.  

Obtener las filas y columnas de una matriz con Scilab

Para obtener las filas de una matriz E=[2,3;1,0] con Scilab
-> E=[2,3;1,0]

 -> E  =

    2.    3.  

    1.    0.  

-> E(1,:) // Primera fila

-> ans  =

    2.    3. 

->E(2,:) /// Segunda fila

 ->ans  =

    1.    0. 

Para obtener las columnas de una matriz E=[2,3;1,0] con Scilab

->E(:,1) // Primera columna

 ans  =

    2.  

    1.  

->E(:,2)  // Segunda columna

 ans  =

    3.  

    0.  

Estrategia basica de control predictivo con Scilab

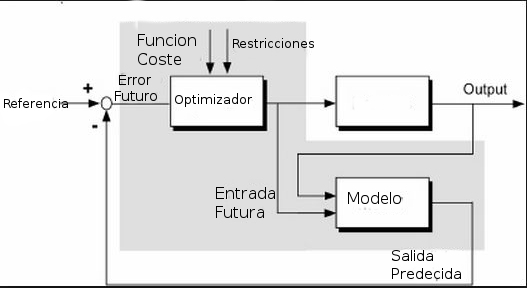
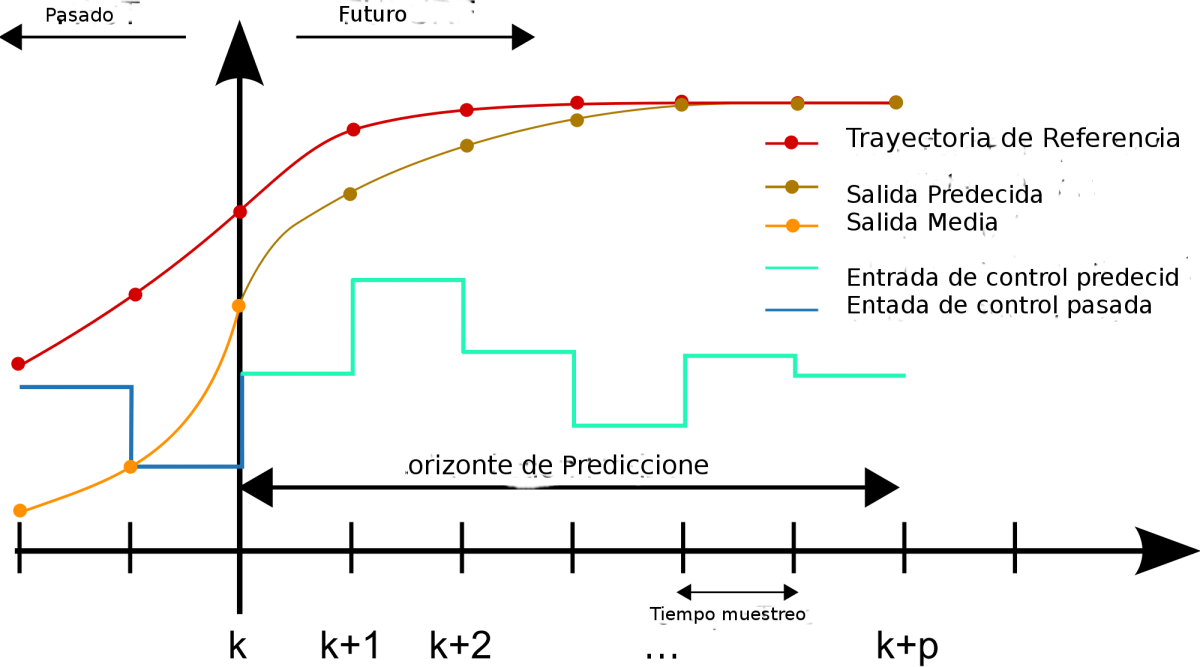
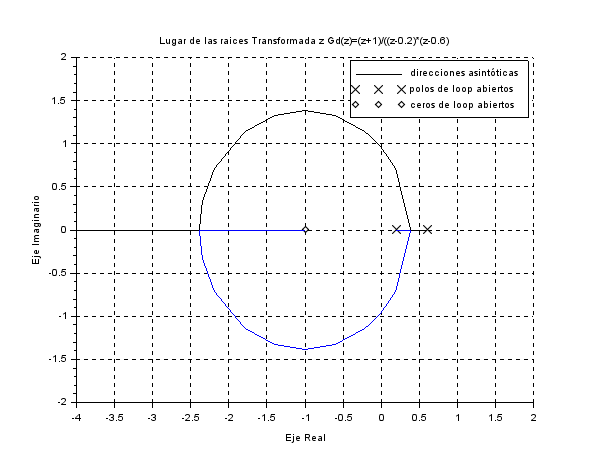
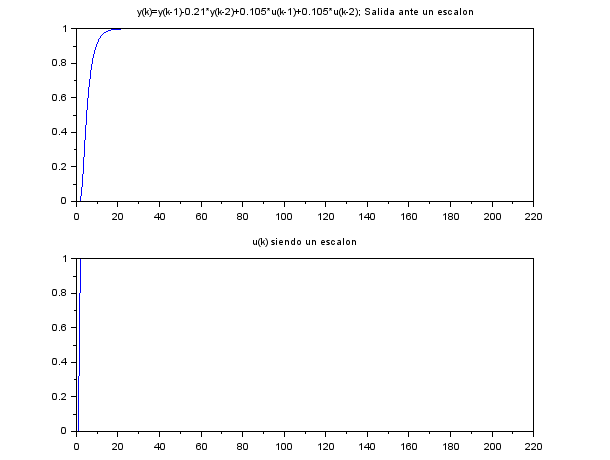
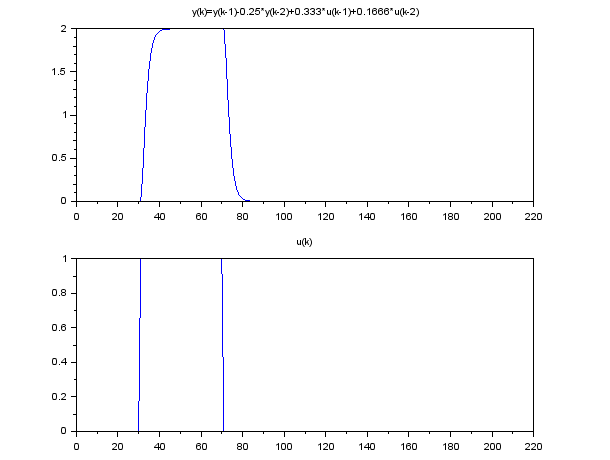
Simulaciones de la estrategia basica de control predictivo con scilab y(k)=y(k-1)-0.25*y(k-2)+0.333*u(k-1)+0.1666*u(k-2)
El proceso normal

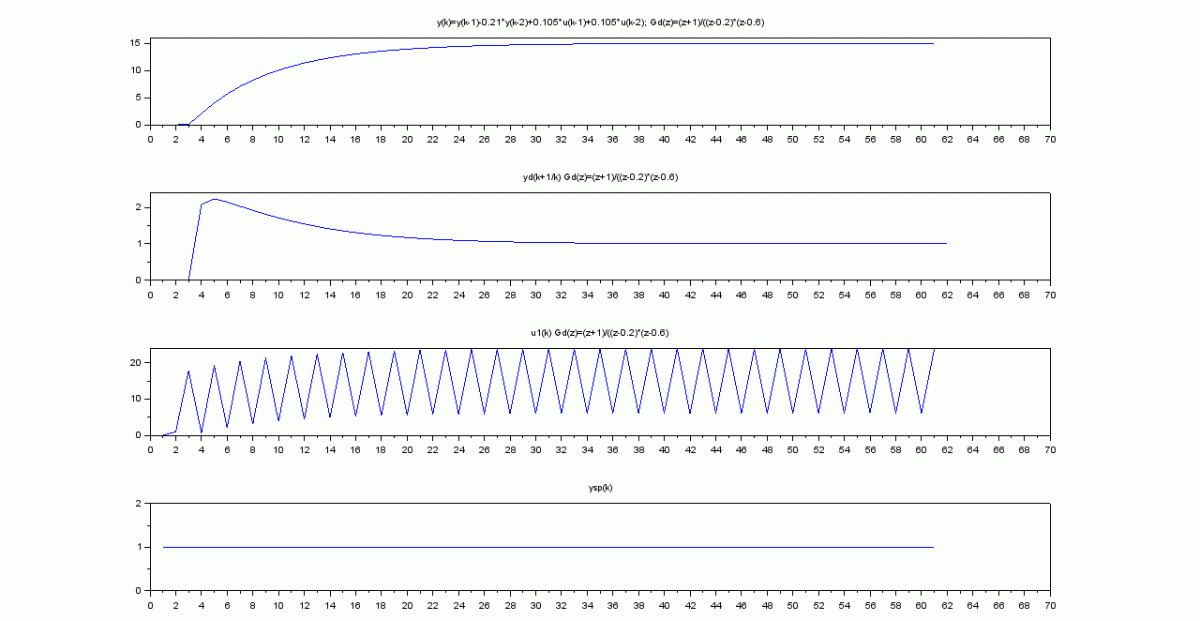
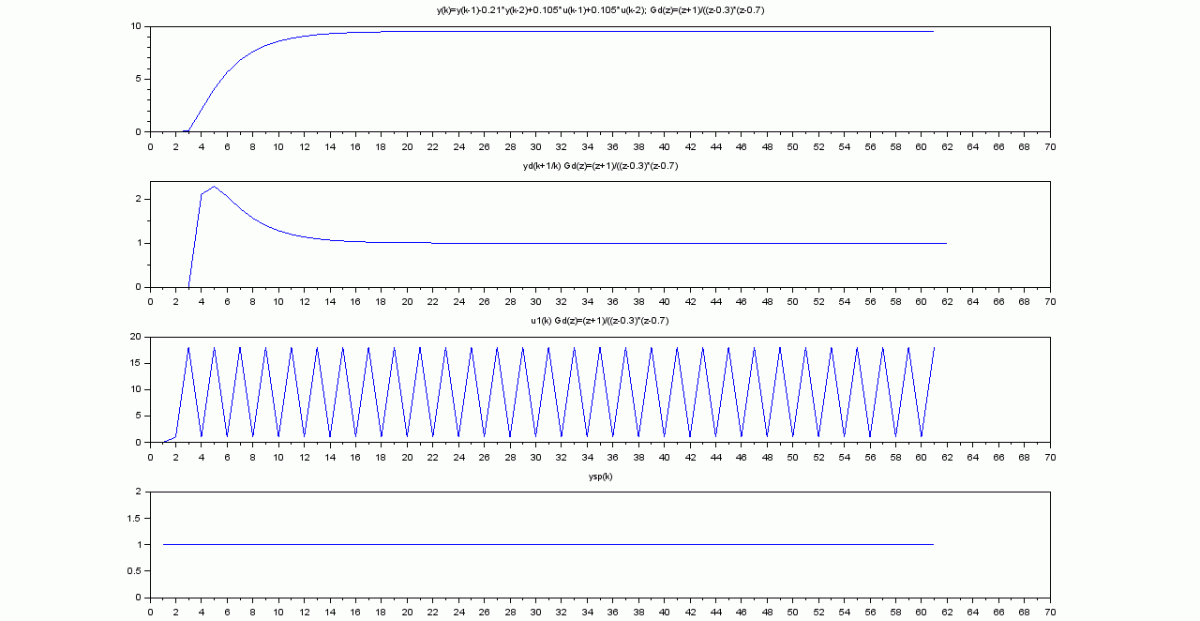
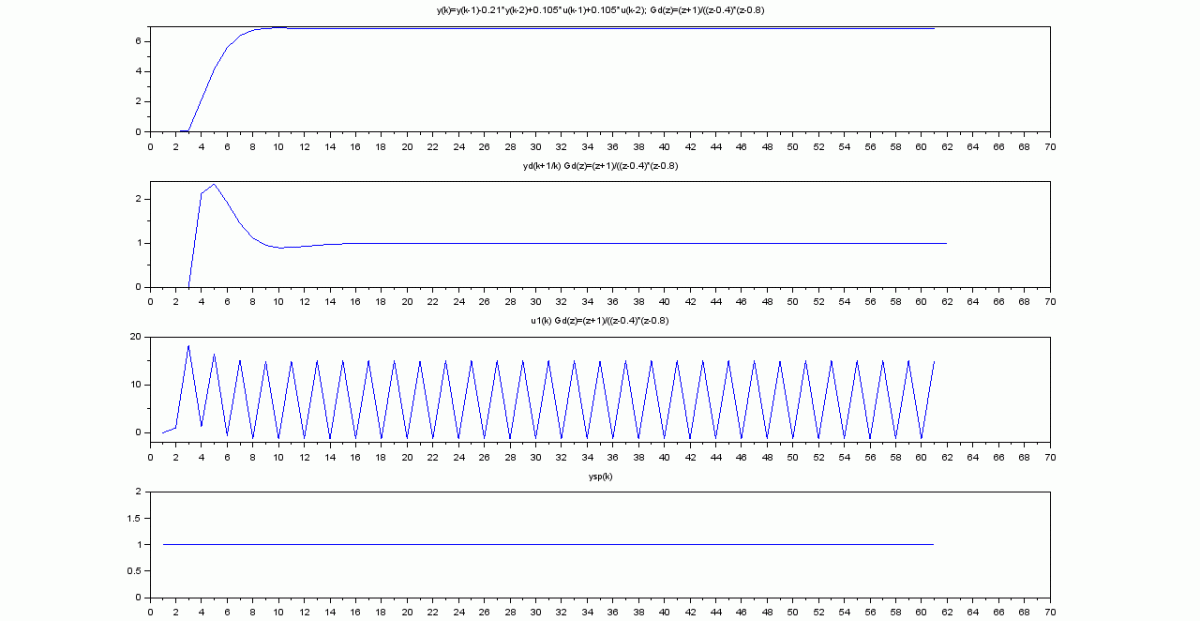
El proceso con control predictivo:


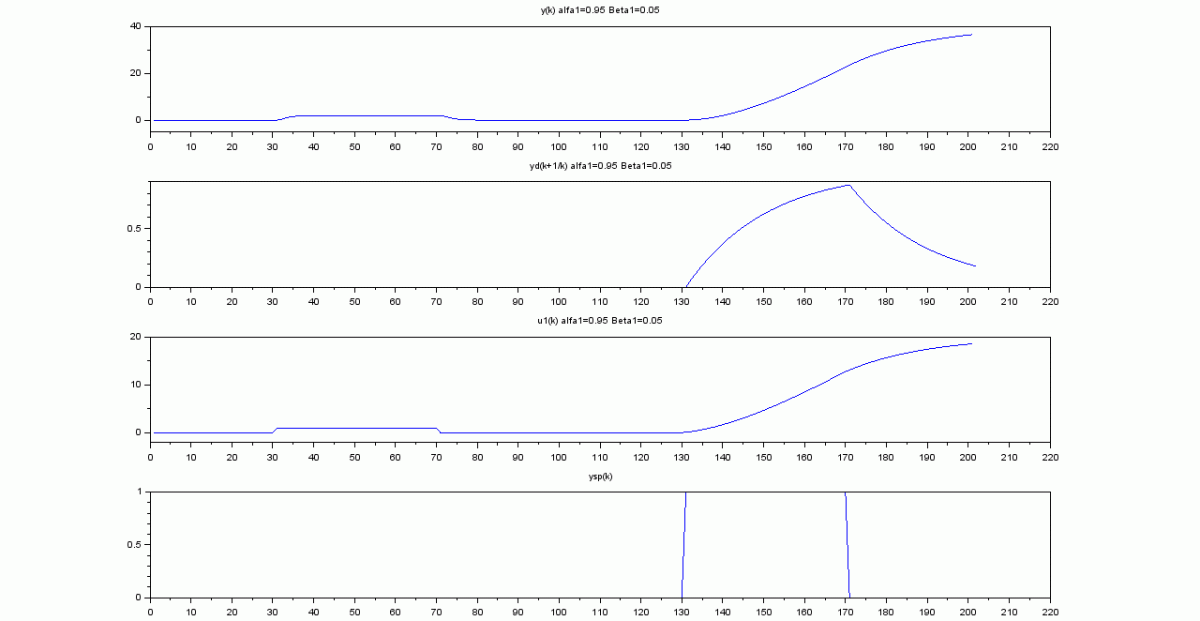
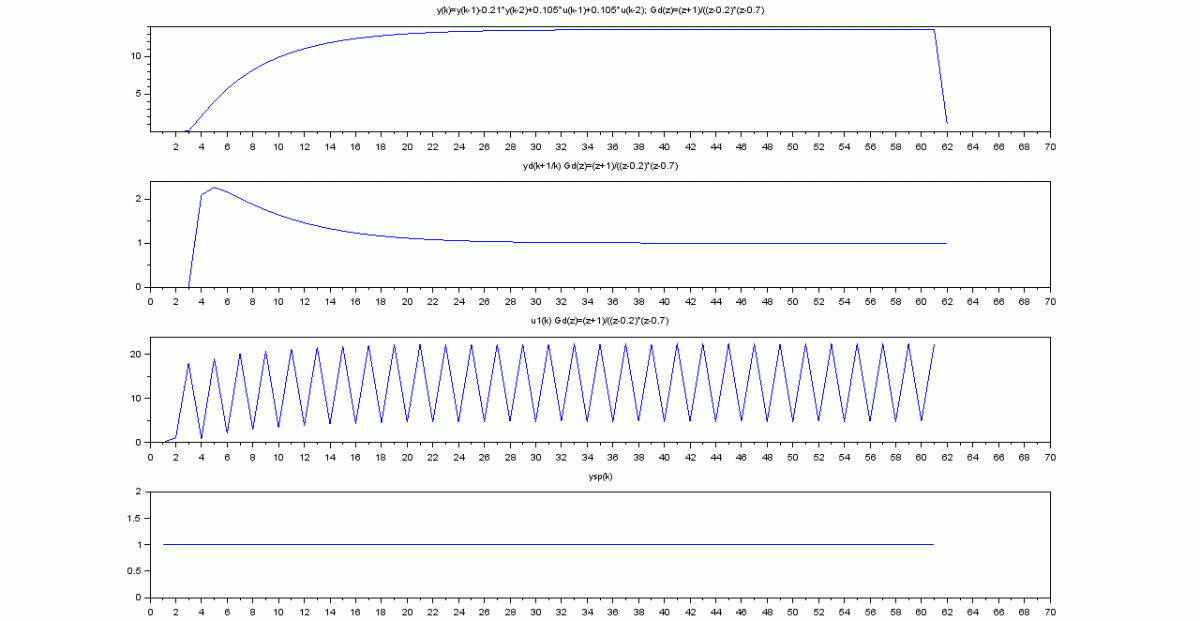
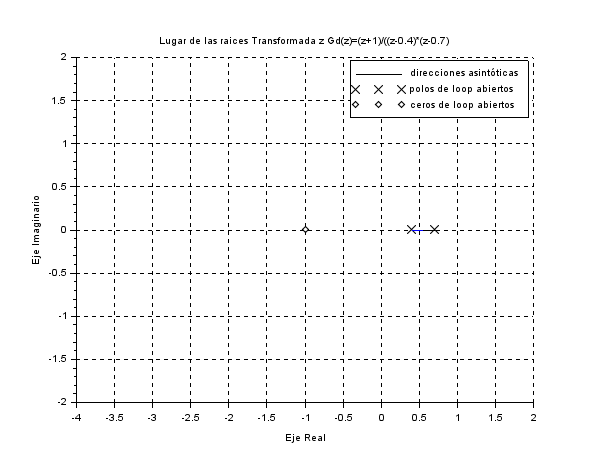
El proceso con control predictivo:

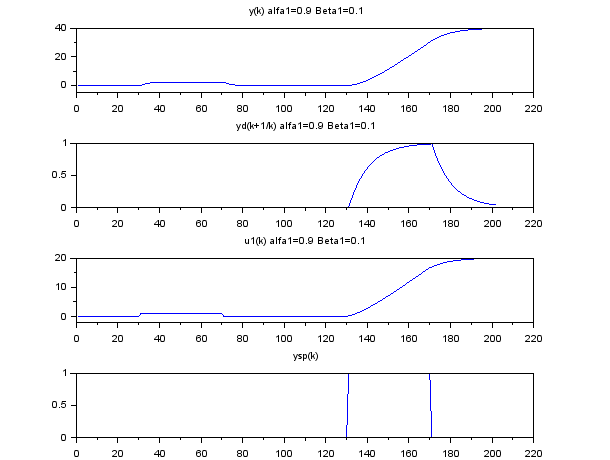
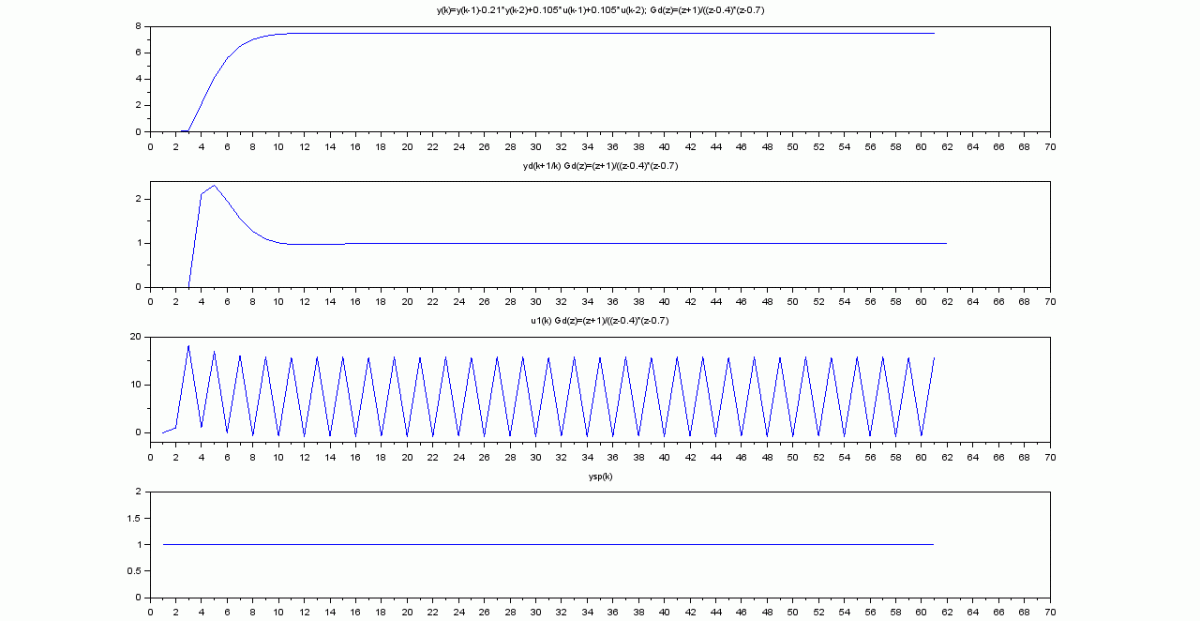
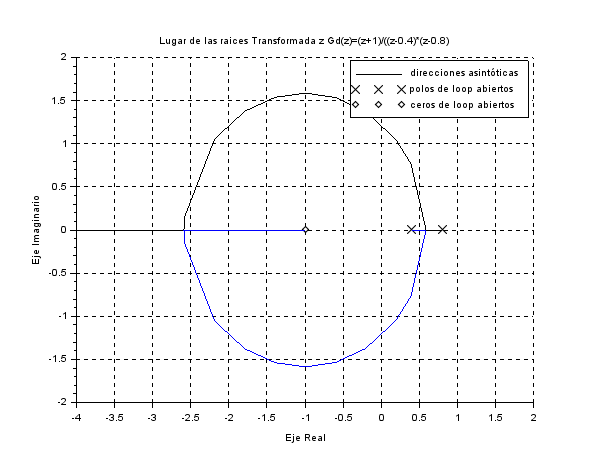
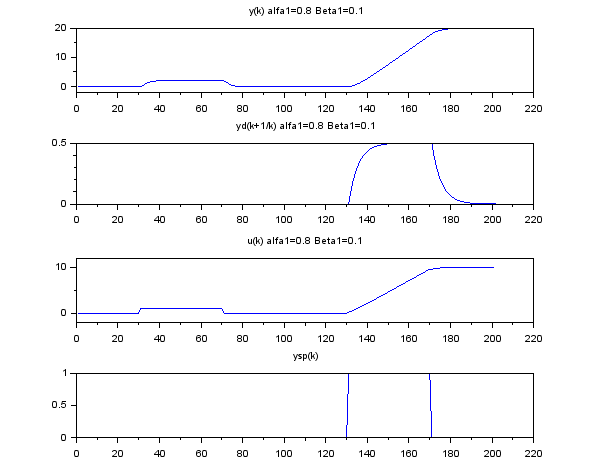
El proceso con control predictivo:

Comparacion para los distintod valores de la salida deseada del control predictivo

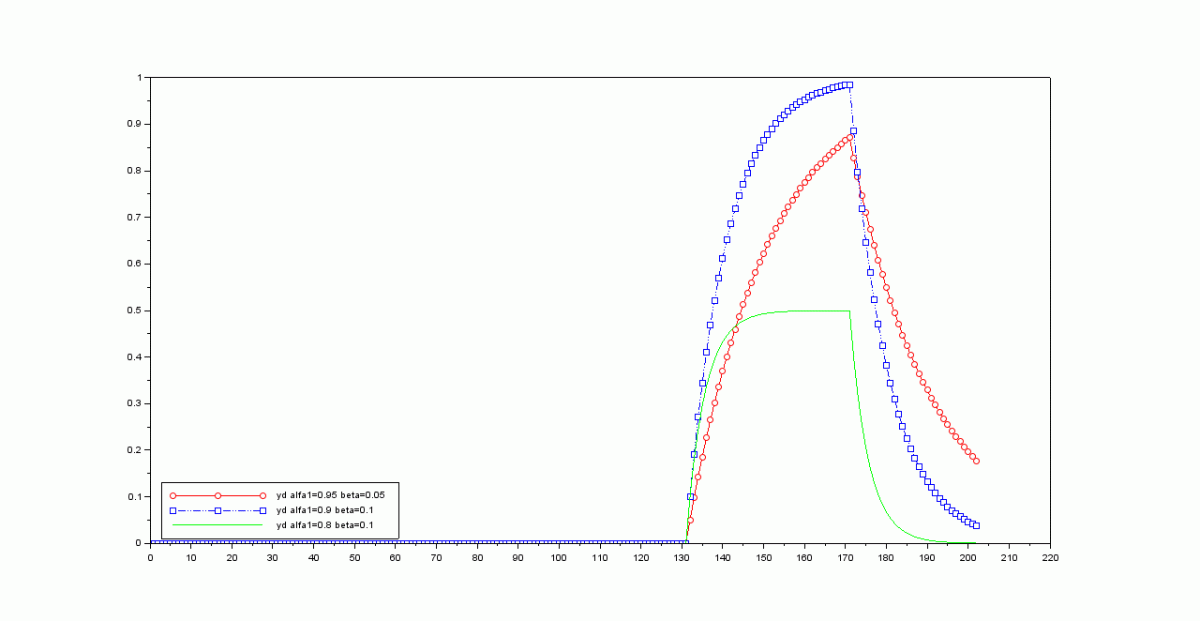
Comparacion para los distintod valores de la salidas obtenidas del control predictivo


Programa en Scilab de la simulacion de la estrategia de control predictivo

clear();

alfa1a=[0.95,0];

beta1a=[0.05,0];

a=[1,-0.25];

b=[0.333,0.1666];

u=[0,zeros(1,29),ones(1,40),zeros(1,131)] //entrada escalon en k=31 y vuelve a 0 en  k=71

y=zeros(1,201);

ysp=[zeros(1,130),ones(1,40),zeros(1,31)] //Comienzo control predictivo consigna valor 0 en k=101, consigna a 1 en k=131 y vuelve a 0 en  k=171

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:201

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)');

subplot(2,1,2)

plot(u);

xtitle('u(k)');

yda=zeros(1,201);

y2a=y;

u2a=u;

yda(100)=y(100);

yda(99)=y(99);

for kt=101:201

    yda(kt+1)=alfa1a(1)*yda(kt)+alfa1a(2)*yda(kt-1)+beta1a(1)*ysp(kt)+beta1a(2)*ysp(kt-1); //Trayectoria deseada

    u2a(1,kt)=(yda(kt+1)-a(1)*y2a(kt)-a(2)*y2a(kt-1)-b(2)*u2a(1,kt-1))/b(1)// Control adaptativo

    y2a(kt)=a(1)*y2a(kt-1)+a(2)*y2a(kt-2)+b(1)*u2a(kt-1)+b(2)*u2a(kt-2)

end

scf(2);

clf(2);

subplot(4,1,1)

plot(y2a);

xtitle('y(k) alfa1=0.95 Beta1=0.05');

subplot(4,1,2)

plot(yda(1,:));

xtitle('yd(k+1/k) alfa1=0.95 Beta1=0.05');

subplot(4,1,3)

plot(u2a);

xtitle('u1(k) alfa1=0.95 Beta1=0.05');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

alfa1b=[0.9,0];

beta1b=[0.1,0];

a=[1,-0.25];

b=[0.333,0.1666];

u=[0,zeros(1,29),ones(1,40),zeros(1,131)] //entrada escalon en k=31 y vuelve a 0 en  k=71

y=zeros(1,201);

ysp=[zeros(1,130),ones(1,40),zeros(1,31)] //Comienzo control predictivo consigna valor 0 en k=101, consigna a 1 en k=131 y vuelve a 0 en  k=171

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:201

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)');

subplot(2,1,2)

plot(u);

xtitle('u(k)');

ydb=zeros(1,201);

y2b=y;

u2b=u;

ydb(100)=y(100);

ydb(99)=y(99);

for kt=101:201

    ydb(kt+1)=alfa1b(1)*ydb(kt)+alfa1b(2)*ydb(kt-1)+beta1b(1)*ysp(kt)+beta1b(2)*ysp(kt-1); //Trayectoria deseada

    u2b(1,kt)=(ydb(kt+1)-a(1)*y2b(kt)-a(2)*y2b(kt-1)-b(2)*u2b(1,kt-1))/b(1)// Control adaptativo

    y2b(kt)=a(1)*y2b(kt-1)+a(2)*y2b(kt-2)+b(1)*u2b(kt-1)+b(2)*u2b(kt-2)

end

scf(3);

clf(3);

subplot(4,1,1)

plot(y2b);

xtitle('y(k) alfa1=0.9 Beta1=0.1');

subplot(4,1,2)

plot(ydb(1,:));

xtitle('yd(k+1/k) alfa1=0.9 Beta1=0.1');

subplot(4,1,3)

plot(u2b);

xtitle('u1(k) alfa1=0.9 Beta1=0.1');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

alfa1c=[0.8,0];

beta1c=[0.1,0];

a=[1,-0.25];

b=[0.333,0.1666];

u=[0,zeros(1,29),ones(1,40),zeros(1,131)] //entrada escalon en k=31 y vuelve a 0 en  k=71

y=zeros(1,201);

ysp=[zeros(1,130),ones(1,40),zeros(1,31)] //Comienzo control predictivo consigna valor 0 en k=101, consigna a 1 en k=131 y vuelve a 0 en  k=171

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:201

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)=y(k-1)-0.25*y(k-2)+0.333*u(k-1)+0.1666*u(k-2)');

subplot(2,1,2)

plot(u);

xtitle('u(k)');

ydc=zeros(1,201);

y2c=y;

u2c=u;

ydc(100)=y(100);

ydc(99)=y(99);

for kt=101:201

    ydc(kt+1)=alfa1c(1)*ydc(kt)+alfa1c(2)*ydc(kt-1)+beta1c(1)*ysp(kt)+beta1c(2)*ysp(kt-1); //Trayectoria deseada

    u2c(1,kt)=(ydc(kt+1)-a(1)*y2c(kt)-a(2)*y2c(kt-1)-b(2)*u2c(1,kt-1))/b(1)// Control adaptativo

    y2c(kt)=a(1)*y2c(kt-1)+a(2)*y2c(kt-2)+b(1)*u2c(kt-1)+b(2)*u2c(kt-2)

end

scf(4);

clf(4);

subplot(4,1,1)

plot(y2c);

xtitle('y(k) alfa1=0.8 Beta1=0.1');

subplot(4,1,2)

plot(ydc(1,:));

xtitle('yd(k+1/k) alfa1=0.8 Beta1=0.1');

subplot(4,1,3)

plot(u2c);

xtitle('u(k) alfa1=0.8 Beta1=0.1');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

scf(5);

clf(5);

x=1:202;

plot(x,yda,'ro-');

plot(x,ydb,'bs:');

plot(x,ydc,'g');

legend(["yd alfa1=0.95 beta=0.05";"yd alfa1=0.9 beta=0.1";"yd alfa1=0.8 beta=0.1"],opt=3);

scf(6);

clf(6);

plot(x,ydb),'b';

scf(6);

clf(6);

x=1:201;

plot(x,y2a,'ro-');

plot(x,y2b,'bs:');

plot(x,y2c,'g');

legend(["y(k) alfa1=0.95 beta=0.05";"y(k) alfa1=0.9 beta=0.1";"y(k) alfa1=0.8 beta=0.1"],opt=2);

Estrategia basica de control predictivo con Scilab y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2)

Lugar de las raices de la transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.6)


Salida del proceso  y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2);  ante  un escalon


El proceso con control predictivo dado los polos y ceros de la transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.6)



Programa en Scilab de la simulacion de la estrategia de control predictivo

clear();

z=%z;

num1=z+1; // Numerador transformada z funcion de tranferencia de la trayectoria deseada

den1=(z-0.2)*(z-0.6); // Denominador transformada z funcion de tranferencia de la trayectoria deseada

gd=syslin('d',num1/den1);

scf(3);

clf(3);

evans(gd); // Lugar de las raices de la Transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.6)

xgrid;

v=[-4 2 -2 2];

mtlb_axis(v);

xgrid

xtitle('Lugar de las raices Transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.6)')

cden=coeff(den1);

cnum=coeff(num1);

alfa1a=[-cden(2),-cden(1)];

beta1a=[cnum(2),cnum(1)];

a=[1,-0.21];

b=[0.105,0.105];

u=[0,ones(1,60)] //entrada escalon 

y=zeros(1,61);

ysp=[ones(1,61)] //Comienzo control predictivo consigna valor 1 en k=1 

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:61

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Salida ante un escalon');

subplot(2,1,2)

plot(u);

xtitle('u(k) siendo un escalon');

yda=zeros(1,61);

y2a=y;

u2a=u;

yda(2)=y(2);

yda(1)=y(1);

for kt=3:61

    yda(kt+1)=alfa1a(1)*y2a(kt)+alfa1a(2)*y2a(kt-1)+beta1a(1)*ysp(kt)+beta1a(2)*ysp(kt-1); //Trayectoria deseada

    u2a(1,kt)=(yda(kt+1)-a(1)*y2a(kt)-a(2)*y2a(kt-1)-b(2)*u2a(1,kt-1))/b(1)// Control adaptativo

    y2a(kt)=a(1)*y2a(kt-1)+a(2)*y2a(kt-2)+b(1)*u2a(kt-1)+b(2)*u2a(kt-2) //Salida con control adaptativo

end

scf(2);

clf(2);

subplot(4,1,1)

plot(y2a);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Gd(z)=(z+1)/((z-0.2)*(z-0.6)');

subplot(4,1,2)

plot(yda(1,:));

xtitle('yd(k+1/k) Gd(z)=(z+1)/((z-0.2)*(z-0.6)');

subplot(4,1,3)

plot(u2a);

xtitle('u1(k) Gd(z)=(z+1)/((z-0.2)*(z-0.6)');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

Lugar de las raices de la transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.7)

Salida del proceso  y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2);  ante  un escalon


El proceso con control predictivo dado los polos y ceros de la transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.7)



Programa en Scilab de la simulacion de la estrategia de control predictivo

clear();

z=%z;

num1=z+1; // Numerador transformada z funcion de tranferencia de la trayectoria deseada

den1=(z-0.2)*(z-0.7); // Denominador transformada z funcion de tranferencia de la trayectoria deseada

gd=syslin('d',num1/den1);

scf(3);

clf(3);

evans(gd); // Lugar de las raices de la Transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.7))

xgrid;

v=[-4 2 -2 2];

mtlb_axis(v);

xgrid

xtitle('Lugar de las raices Transformada z Gd(z)=(z+1)/((z-0.2)*(z-0.7)')

cden=coeff(den1);

cnum=coeff(num1);

alfa1a=[-cden(2),-cden(1)];

beta1a=[cnum(2),cnum(1)];

a=[1,-0.21];

b=[0.105,0.105];

u=[0,ones(1,60)] //entrada escalon 

y=zeros(1,61);

ysp=[ones(1,61)] //Comienzo control predictivo consigna valor 1 en k=1 

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:201

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Salida ante un escalon');

subplot(2,1,2)

plot(u);

xtitle('u(k) siendo un escalon');

yda=zeros(1,61);

y2a=y;

u2a=u;

yda(2)=y(2);

yda(1)=y(1);

for kt=3:61

    yda(kt+1)=alfa1a(1)*y2a(kt)+alfa1a(2)*y2a(kt-1)+beta1a(1)*ysp(kt)+beta1a(2)*ysp(kt-1); //Trayectoria deseada

    u2a(1,kt)=(yda(kt+1)-a(1)*y2a(kt)-a(2)*y2a(kt-1)-b(2)*u2a(1,kt-1))/b(1)// Control adaptativo

    y2a(kt)=a(1)*y2a(kt-1)+a(2)*y2a(kt-2)+b(1)*u2a(kt-1)+b(2)*u2a(kt-2) //Salida con control adaptativo

end

scf(2);

clf(2);

subplot(4,1,1)

plot(y2a);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Gd(z)=(z+1)/((z-0.2)*(z-0.7)');

subplot(4,1,2)

plot(yda(1,:));

xtitle('yd(k+1/k) Gd(z)=(z+1)/((z-0.2)*(z-0.7)');

subplot(4,1,3)

plot(u2a);

xtitle('u1(k) Gd(z)=(z+1)/((z-0.2)*(z-0.7)');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

Lugar de las raices de la transformada z Gd(z)=(z+1)/((z-0.3)*(z-0.7)

Salida del proceso  y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2);  ante  un escalon


El proceso con control predictivo dado los polos y ceros de la transformada z Gd(z)=(z+1)/((z-0.3)*(z-0.7)



Programa en Scilab de la simulacion de la estrategia de control predictivo

clear();

z=%z;

num1=z+1; // Numerador transformada z funcion de tranferencia de la trayectoria deseada

den1=(z-0.3)*(z-0.7); // Denominador transformada z funcion de tranferencia de la trayectoria deseada

gd=syslin('d',num1/den1);

scf(3);

clf(3);

evans(gd); // Lugar de las raices de la Transformada z Gd(z)=(z+1)/((z-0.3)*(z-0.7))

xgrid;

v=[-4 2 -2 2];

mtlb_axis(v);

xgrid

xtitle('Lugar de las raices Transformada z Gd(z)=(z+1)/((z-0.3)*(z-0.7)')

cden=coeff(den1);

cnum=coeff(num1);

alfa1a=[-cden(2),-cden(1)];

beta1a=[cnum(1),cnum(1)];

a=[1,-0.21];

b=[0.105,0.105];

u=[0,ones(1,60)] //entrada escalon 

y=zeros(1,61);

ysp=[ones(1,61)] //Comienzo control predictivo consigna valor 1 en k=1 

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:61

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Salida ante un escalon');

subplot(2,1,2)

plot(u);

xtitle('u(k) siendo un escalon');

yda=zeros(1,61);

y2a=y;

u2a=u;

yda(2)=y(2);

yda(1)=y(1);

for kt=3:61

    yda(kt+1)=alfa1a(1)*y2a(kt)+alfa1a(2)*y2a(kt-1)+beta1a(1)*ysp(kt)+beta1a(2)*ysp(kt-1); //Trayectoria deseada

    u2a(1,kt)=(yda(kt+1)-a(1)*y2a(kt)-a(2)*y2a(kt-1)-b(2)*u2a(1,kt-1))/b(1);// Control adaptativo

    y2a(kt)=a(1)*y2a(kt-1)+a(2)*y2a(kt-2)+b(1)*u2a(kt-1)+b(2)*u2a(kt-2); //Salida con control adaptativo

end

scf(2);

clf(2);

subplot(4,1,1)

plot(y2a);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Gd(z)=(z+1)/((z-0.3)*(z-0.7)');

subplot(4,1,2)

plot(yda(1,:));

xtitle('yd(k+1/k) Gd(z)=(z+1)/((z-0.3)*(z-0.7)');

subplot(4,1,3)

plot(u2a);

xtitle('u1(k) Gd(z)=(z+1)/((z-0.3)*(z-0.7)');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

Lugar de las raices de la transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.7)

Salida del proceso  y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2);  ante  un escalon


El proceso con control predictivo dado los polos y ceros de la transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.7)



Programa en Scilab de la simulacion de la estrategia de control predictivo

clear();

z=%z;

num1=z+1; // Numerador transformada z funcion de tranferencia de la trayectoria deseada

den1=(z-0.4)*(z-0.7); // Denominador transformada z funcion de tranferencia de la trayectoria deseada

gd=syslin('d',num1/den1);

scf(3);

clf(3);

evans(gd); // Lugar de las raices de la Transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.7))

xgrid;

v=[-4 2 -2 2];

mtlb_axis(v);

xgrid

xtitle('Lugar de las raices Transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.7)')

cden=coeff(den1);

cnum=coeff(num1);

alfa1a=[-cden(2),-cden(1)];

beta1a=[cnum(1),cnum(1)];

a=[1,-0.21];

b=[0.105,0.105];

u=[0,ones(1,60)] //entrada escalon 

y=zeros(1,61);

ysp=[ones(1,61)] //Comienzo control predictivo consigna valor 1 en k=1 

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:61

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Salida ante un escalon');

subplot(2,1,2)

plot(u);

xtitle('u(k) siendo un escalon');

yda=zeros(1,61);

y2a=y;

u2a=u;

yda(2)=y(2);

yda(1)=y(1);

for kt=3:61

    yda(kt+1)=alfa1a(1)*y2a(kt)+alfa1a(2)*y2a(kt-1)+beta1a(1)*ysp(kt)+beta1a(2)*ysp(kt-1); //Trayectoria deseada

    u2a(1,kt)=(yda(kt+1)-a(1)*y2a(kt)-a(2)*y2a(kt-1)-b(2)*u2a(1,kt-1))/b(1);// Control adaptativo

    y2a(kt)=a(1)*y2a(kt-1)+a(2)*y2a(kt-2)+b(1)*u2a(kt-1)+b(2)*u2a(kt-2); //Salida con control adaptativo

end

scf(2);

clf(2);

subplot(4,1,1)

plot(y2a);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Gd(z)=(z+1)/((z-0.4)*(z-0.7)');

subplot(4,1,2)

plot(yda(1,:));

xtitle('yd(k+1/k) Gd(z)=(z+1)/((z-0.4)*(z-0.7)');

subplot(4,1,3)

plot(u2a);

xtitle('u1(k) Gd(z)=(z+1)/((z-0.4)*(z-0.7)');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');

Lugar de las raices de la transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.8)

Salida del proceso  y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2);  ante  un escalon


El proceso con control predictivo dado los polos y ceros de la transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.8)



Programa en Scilab de la simulacion de la estrategia de control predictivo

clear();

z=%z;

num1=z+1; // Numerador transformada z funcion de tranferencia de la trayectoria deseada

den1=(z-0.4)*(z-0.8); // Denominador transformada z funcion de tranferencia de la trayectoria deseada

gd=syslin('d',num1/den1);

scf(3);

clf(3);

evans(gd); // Lugar de las raices de la Transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.8))

xgrid;

v=[-4 2 -2 2];

mtlb_axis(v);

xgrid

xtitle('Lugar de las raices Transformada z Gd(z)=(z+1)/((z-0.4)*(z-0.8)')

cden=coeff(den1);

cnum=coeff(num1);

alfa1a=[-cden(2),-cden(1)];

beta1a=[cnum(2),cnum(1)];

a=[1,-0.21];

b=[0.105,0.105];

u=[0,ones(1,60)] //entrada escalon 

y=zeros(1,61);

ysp=[ones(1,61)] //Comienzo control predictivo consigna valor 1 en k=1 

y(1)=0;

u(1)=0;

y(2)=0;

for k=3:61

    y(k)=a(1)*y(k-1)+a(2)*y(k-2)+b(1)*u(k-1)+b(2)*u(k-2); //Salida del proceso

end

y

scf(1);

clf(1);

subplot(2,1,1)

plot(y);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Salida ante un escalon');

subplot(2,1,2)

plot(u);

xtitle('u(k) siendo un escalon');

yda=zeros(1,61);

y2a=y;

u2a=u;

yda(2)=y(2);

yda(1)=y(1);

for kt=3:61

    yda(kt+1)=alfa1a(1)*y2a(kt)+alfa1a(2)*y2a(kt-1)+beta1a(1)*ysp(kt)+beta1a(2)*ysp(kt-1); //Trayectoria deseada

    u2a(1,kt)=(yda(kt+1)-a(1)*y2a(kt)-a(2)*y2a(kt-1)-b(2)*u2a(1,kt-1))/b(1);// Control adaptativo

    y2a(kt)=a(1)*y2a(kt-1)+a(2)*y2a(kt-2)+b(1)*u2a(kt-1)+b(2)*u2a(kt-2); //Salida con control adaptativo

end

scf(2);

clf(2);

subplot(4,1,1)

plot(y2a);

xtitle('y(k)=y(k-1)-0.21*y(k-2)+0.105*u(k-1)+0.105*u(k-2); Gd(z)=(z+1)/((z-0.4)*(z-0.8)');

subplot(4,1,2)

plot(yda(1,:));

xtitle('yd(k+1/k) Gd(z)=(z+1)/((z-0.4)*(z-0.8)');

subplot(4,1,3)

plot(u2a);

xtitle('u1(k) Gd(z)=(z+1)/((z-0.4)*(z-0.8)');

subplot(4,1,4)

plot(ysp);

xtitle('ysp(k)');