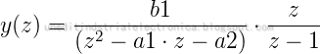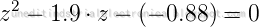Operaciones con variables:
Visualizar una variable. Operador:
disp()
Comparar numeros reales o complejos con una tolerancia. 0 si son iguales , 1 y -1 si son distintos. Para variables solo vale 7 cifras de precision . Operador:
assert_comparecomplex( )
assert_comparecomplex( 1.002,1.000002,1.e-2 ) //2cifras de precision.
Operaciones con matrices:
Traspuesta de una matriz con Scilab. Operador:
'
[1 2; 1 3]'
Dibujar:
Leyendas de las funciones dibujadas con Scilab. Operador:
legend()
legend(['cos(t)';'cos(2*t)';'cos(3*t)']);
Limites de los ejes en Scilab:
a=gca() ;//Obtiene los ejes
a.box="on";
a.data_bounds=[-1.5,-1.5;1.5,1.5]; //define los limites inferiores y superiores eje x , eje y
Elegir ventana en Scilab. Operador
scf()
scf(1)\\ Ventana 1
Borrar ventana en Scilab. Operador
clf()
clf(1)\\ Borrar ventana 1
Operaciones con polinomios:
Calcular el numerador de un polinomio. Operador:
numer()
Calcular el denominador de un polinomio. Operador:
denom()
Calcular la derivada de un polinomio. Operador:
derivat()
Sustituir valor en polinomio. Operador:
horner()
horner("polinomio", "valor")
Operaciones de consola:
Limpiar consola. Operador:
clc